카메라 캘리브레이션 (Camera Calibration)
우리가 실제 눈으로 보는 세상은 3차원이다. 이것을 카메라로 찍으면 2차원의 이미지로 변한다.
3차원의 점들이 이미지 상에서 어디에 맺히는지 생각하면 영상을 찍을 당시의 카메라의 위치 및 방향에 의해 결정된다.
하지만 실제 이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 카메라 내부의 기구적인 부분에 의해서 크게 영향을 받는다.
따라서 3차원 점들이 영상에 투영된 위치를 구하거나 역으로 영상좌표로부터 3차원 공간좌표를 복원할 때에는 이러한 내부 요인을 제거해야 계산이 가능해집니다.
이러한 내부 요인의 파라미터 값을 구하는 과정을 캘리브레이션이라고 한다.
카메라 영상은 3차원 공간상의 점들을 2차원 이미지 평면에 투사함으로써 얻어진다.

여기서 X,Y,Z는 월드 좌표계 상의 3D 점의 좌표, [R | t]는 월드 좌표계를 카메라 좌표계로 변환시키기 위한 회전/이동변환 행렬이며 A는 intrinsic camera matrix(내부 파라미터) 이다.
intrinsic parameter (내부 파라미터)
초점거리(focal length) : fx, fy, 주점(principal point): cx, cy, 비대칭계수(skew coefficient): skew_c = tanα
초점거리 (focal length)
흔히 볼록렌즈의 초점을 생각하기 쉬운데, 여기서 말하는 초점거리는 렌즈중심과 이미지센서(CCD, CMOS 등)와의 거리를 말합니다.
CCD ( CCD란 Charge Coupled Device의 약칭이다. CCD에는 많은 수의 광다이오드 소자가 집적되어 있고 이곳에 빛이 비추어지면 빛의 양에 따라 전자가 발생하고 그 전자가 생성된 량(量)에 따라 화상(이미지)이 생겨난다. CCD 이미지 센서는 치수나 화질 등의 여러 종류가 있으며, 디지털 카메라를 비롯하여 스캐너나 휴대전화, 자동차, 미사일의 센서 등에 폭넓게 쓰인다. 좋은 화질의 화상(이미지)을 얻기 위해서는 CCD가 클수록 좋다.)
CMOS( CMOS 이미지 센서 원리는 1960년대 후반 고안되었으나, MOS 기술이 첨단화 된 1990년대 이후 실용화 되었다. CCD에 비해 감도가 낮고 노이즈 영향을 잘 받기 때문에 이미지 센서로는 CMOS보다 CCD가 더 많이 채용되었다. 하지만 이후 상대적 약점인 노이즈 문제가 온칩 노이즈 제거 기술 등을 이용하여 해결되기 시작하면서, 2000년대 이후 DSLR 카메라에 이미지 센서로 채택되기 시작하였다. 2014년 전체 이미지 센서의 수량 중 CMOS의 점유율은 96%였다.)
디지털 카메라에서 초점거리는 mm단위로 표현되지만 카메라 모델에서 말하는 초점거리(f)는 픽셀(pixel) 단위로 표현됩니다. 즉 f의 단위로로 픽셀이라는 의미입니다.
이미지 픽셀은 이미지 센서의 셀에 대응되기 때문에, 초점거리가 픽셀단위라는 의미는 초점거리가 이미지 센서의 셀 크기에 대한 상대적인 값으로 표현된다는 의미이다.
ex) 이미지 센서의 셀의 크기가 0.1mm이고 카메라의 초점거리가 500pixel이라고 하면 이 카메라의 렌즈 중심에서 이미지 센서까지의 거리는 이미지 센서 셀 크기의 500배 즉, 50mm라는 의미이다.
카메라 모델에서 초점거리를 하나의 값으로 f라 표현하지 않고, fx, fy로 구분하여 표현하는 경우가 있다. (실제로 캘리브레이션을 수행하면 fx, fy를 구분하여 반환된다.)
이는 이미지 센서의 물리적인 셀 간격이 가로 방향과 세로 방향이 서로 다를 수 있음을 모델링하기 위함이다. 이 경우 fx는 초점거리가 가로 방향 셀 크기의 몇 배인지를 나타내고 fy는 초점거리가 세로 방향 센서 셀 크기의 몇 배인지를 나타냅니다. fx 와 fy 모두 단위는 픽셀이며 현대의 일반적인 카메라는 가로방향 셀 간격과 세로방향 셀 간격의 차이가 없기 때문에 f = fx = fy라 놓아도 무방합니다.
캘리브레이션을 수행할 때 이미지 해상도를 1/2로 낮추면 캘리브레이션 결과의 초점거리도 1/2로 작아진다. 실제 물리적 초점거리가 변하는 것은 아니지만 카메라 모델에서의 초점거리는 상대적인 개념이기 때문에 해상도를 바꾸면 학 픽셀에 대응하는 물리크기가 변하고 따라서 초점거리도 변하게 된다

초점으로부터 거리가 1(unit distance)의 평면을 normalized image plane이라고 부르며 이 평면상의 좌표를 보통 normalized image coordinate라고 부른다. 이것은 실제로 존재하지 않는 가상의 이미지 평면이다. 카메라 좌표계 상의 한 점 (Xc, Yc, Zc)를 영상좌표계로 변환할 때 먼저 Xc, Yc, Zc(카메라 초점에서의 거리)로 나누는 것은 이 normalized image plane 상의 좌표로 변환하는 것이며, 여기에 다시 초점거리 f를 곱하면 우리가 원하는 이미지 평면에서의 영상좌표가 나온다. 그런데 이미지에서 픽셀좌표는 이미지의 중심이 아닌 이미지의 좌상단 모서리를 기준(원점)으로 하기 때문에 실제 최종적인 영상좌표는 여기에 (cx, cy)를 더한 값이 된다.
즉 x = fxX/Z + cx, y = fyY/Z + cy이다.
주점 (principal point)
주점 cx, cy는 카메라 렌즈의 중심 즉, 핀홀에서 이미지 센서에 내린 수선의 발의 영상좌표로서 일반적으로 말하는 영상 줌싱점과는 다른 의미이다.
비대칭 계수 (skew coefficient)
비대칭 계수 skew_c는 이미지 센서의 cell array의 y축이 기울어진 정도를 나타낸다.
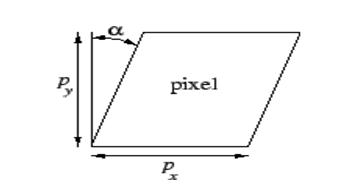
요즘 카메라들은 이러한 skew 에러가 거의 없기 때문에 비대칭 계수까지 고려하지 않는다고 한다. skew_c = 0
extrinsic parameters (카메라 외부 파라미터)
카메라 외부 파라미터는 카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터이다.
두 좌표계 사이의 회전(rotation) 및 평행이동(translation)변환으로 표현된다.
카메라 외부 파라미터는 카메라 고유의 파라미터가 아니기 때문에 카메라를 어떤 위치에 어떤 방향으로 설치했는지에 따라 달라지고 또한 월드 좌표계를 어떻게 정의했느냔에 따라서 달라진다.
카메라 외부 파라미터를 구하기 위해서는 먼저 캘리브레이션등을 이용하여 카메라 고유의 내부 파라미터들을 구하고, 미리 알고 있는 3D월드좌표 2D영상좌표 매칭 쌍들을 이용하여 맨 위의 식에서 변환행렬을 구하면 된다. OpenCV에 있는 solvePnP함수를 이용하면 이러한 계산을 쉽게 할 수 있다.
먼저 카메라로 체커보드를 최소 3장 이상 찍는다. 많으면 많을수록 좋다고 한다.

체커보드를 고정시켜놓고 여러 관점에서 사진을 찍는다.
import cv2
import numpy as np
import os
import glob
# 체커보드의 차원 정의
CHECKERBOARD = (6,8) # 체커보드 행과 열당 내부 코너 수
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 각 체커보드 이미지에 대한 3D 점 벡터를 저장할 벡터 생성
objpoints = []
# 각 체커보드 이미지에 대한 2D 점 벡터를 저장할 벡터 생성
imgpoints = []
# 3D 점의 세계 좌표 정의
objp = np.zeros((1, CHECKERBOARD[0] * CHECKERBOARD[1], 3), np.float32)
objp[0,:,:2] = np.mgrid[0:CHECKERBOARD[0], 0:CHECKERBOARD[1]].T.reshape(-1, 2)
prev_img_shape = None
# 주어진 디렉터리에 저장된 개별 이미지의 경로 추출
images = glob.glob('/home/jaewoong/opencv_calibration/images/*.jpg')
for fname in images:
img = cv2.imread(fname)
# 그레이 스케일로 변환
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 체커보드 코너 찾기
# 이미지에서 원하는 개수의 코너가 발견되면 ret = true
ret, corners = cv2.findChessboardCorners(gray,
CHECKERBOARD,
cv2.CALIB_CB_ADAPTIVE_THRESH + cv2.CALIB_CB_FAST_CHECK + cv2.CALIB_CB_NORMALIZE_IMAGE)
# 원하는 개수의 코너가 감지되면,
# 픽셀 좌표 미세조정 -> 체커보드 이미지 표시
if ret == True:
objpoints.append(objp)
# 주어진 2D 점에 대한 픽셀 좌표 미세조정
corners2 = cv2.cornerSubPix(gray, corners, (11,11),(-1,-1), criteria)
imgpoints.append(corners2)
# 코너 그리기 및 표시
img = cv2.drawChessboardCorners(img, CHECKERBOARD, corners2, ret)
cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()
h,w = img.shape[:2] # 480, 640
# 알려진 3D 점(objpoints) 값과 감지된 코너의 해당 픽셀 좌표(imgpoints) 전달, 카메라 캘리브레이션 수행
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
print("Camera matrix : \\n") # 내부 카메라 행렬
print(mtx)
print("dist : \\n") # 렌즈 왜곡 계수(Lens distortion coefficients)
print(dist)
# print("rvecs : \\n") # 회전 벡터
# print(rvecs)
# print("tvecs : \\n") # 이동 벡터
# print(tvecs)

images 파일의 모든 jpg 파일에 대해 캘리브레이션을 진행한다.
images calibration
Camera matrix :
[[608.26617185 0. 328.29683812]
[ 0. 609.86764559 238.40459802]
[ 0. 0. 1. ]]
dist :
[[ 2.02438415e-02 6.13472913e-01 -1.20950082e-03 -1.98880472e-04
-2.38263200e+00]]
이렇게 내부 파라미터 값이 나왔고,
위의 내부 파라미터 값을 solvpnp 코드에 입력을 하여 외부파라미터 값을 구한다.
사실 위 cv2.calibrateCamera 함수에서 반환하는 값들은 내부파라미터와 왜곡 계수도 있지만
외부파라미터의 회전, 이동 벡터도 포함되어있다.
여기서 반환되는 외부파라미터는 월드 좌표계 기준에서 카메라의 이동 및 회전을 나타내는 값이다.
다음은 Solvepnp를 이용해서 외부파라미터를 구하는 방법이다.
영상으로부터 카메라의 위치 및 자세를 계산하려면 다음과 같은 전제 조건이 필요합니다.
- 해당 카메라에 대한 내부 파라미터(intrinsic parameters) 및 왜곡계수을 알고 있어야 함: fx, fy, cx, cy, k1, k2, p1, p2
- 물체에 대한 최소 4개 이상의 3D 월드좌표와 이에 대응되는 2D 영상좌표 쌍
예를 들어, 아래 그림과 같이 한변의 길이가 1인 사각형 마크를 바닥에 놓고 카메라로 영상을 획득했을 때 각각의 사각형 꼭지점들에 대한 영상좌표를 구한 후, 사각형 꼭지점들의 3D 월드좌표와 2D 영상좌표 쌍들을 solvePnP 함수에 넣어주면 카메라의 위치 및 자세정보가 나옵니다.

그림에서는 사각형 마크의 월드좌표를 (0,0,0), (1,0,0), (0,1,0), (1,1,0)로 설정해 주었지만 만일 마크를 기준으로 월드좌표계를 설정하지 않고 별도의 월드좌표계를 설정(예를 들어 방의 한쪽 모서리를 원점으로 설정)하고자 할 때에는 해당 좌표계를 기준으로 한 좌표를 마크의 월드좌표로 입력해 주면 됩니다. 그러면 solvePnP 함수에서는 설정한 월드좌표계를 기준으로 한 카메라의 위치 및 자세정보를 반환하게 됩니다.
자 그럼 3D 월드 좌표는 위 사각형이 평면에 있다고 가정을 하고 z값을 0으로 두고 얻을 수 있다.
그리도 2D 영상좌표는 체커보드를 사용하면 모서리를 감지해 바로 얻을 수 있지만 체커보드를 사용하지 않으면 그 이미지의 픽셀 좌표를 사용하면 된다.
import cv2
def onMouse(event, x, y, flags, param) :
if event == cv2.EVENT_LBUTTONDOWN :
print('왼쪽 마우스 클릭 했을 때 좌표 : ', x, y)
img = cv2.imread('/home/jaewoong/realsense_image/point(new)/d435_0.jpg')
cv2.imshow('image', img)
cv2.setMouseCallback('image', onMouse)
cv2.waitKey()
위 코드는 이미지를 클릭했을 때 마우스에 해당하는 픽셀 좌표를 디버깅 하는 코드이다.
그럼 이 픽셀 좌표와 3D 월드 좌표를 대응 시키고 카메라 내부파라미터와 왜곡계수를 이용하여 solvepnp 함수를 사용하면 외부파라미터를 구할 수 있다.
solvepnp의 함수를 이용한 c++코드이다.
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main(int argc, char **argv)
{
// Read input image
cv::Mat im = cv::imread("/home/jaewoong/opencv_calibration/left_image.jpg");
// cv::resize( im, im, cv::Size( im.cols/2, im.rows/2 ), 0, 0, cv::INTER_AREA);
cv::resize( im, im, cv::Size( im.cols, im.rows ), 0, 0, cv::INTER_AREA);
// 2D image points. If you change the image, you need to change vector
std::vector<cv::Point2d> image_points;
image_points.push_back( cv::Point2d(485,533) ); // 1280, 720
image_points.push_back( cv::Point2d(604,537) );
image_points.push_back( cv::Point2d(602,621) );
image_points.push_back( cv::Point2d(457,618) );
image_points.push_back( cv::Point2d(538,574) );
// 3D model points.
std::vector<cv::Point3d> model_points;
model_points.push_back(cv::Point3d(-2.0, 2.0, 0.0));
model_points.push_back(cv::Point3d(2.0, 2.0, 0.0)); // Nose tip
model_points.push_back(cv::Point3d(2.0, -2.0, 0.0)); // Chin
model_points.push_back(cv::Point3d(-2.0, -2.0, 0.0)); // Left eye left corner
model_points.push_back(cv::Point3d(0.0, 0.0, 0.0)); // Right eye right corner
// Left Mouth corner // Right mouth corner
// Camera internals
// double focal_length = im.cols; // Approximate focal length.
// Point2d center = cv::Point2d(im.cols/2,im.rows/2);
// cv::Mat camera_matrix = (cv::Mat_<double>(3,3) << 350.6575012207031, 0.0, 318.9624938964844, 0.0, 350.6575012207031, 190.42774963378906, 0.0, 0.0, 1.0); 640,360
// cv::Mat dist_coeffs = (cv::Mat_ <double>(4,1) << -0.17287799715995f, 0.026074500754475594f, 0.0, -9.226740075973794e-05); // Assuming no lens distortion
cv::Mat camera_matrix = (cv::Mat_<double>(3,3) << 712.54130286, 0.0, 639.67904873, 0.0, 714.09302856, 382.31150295, 0.0, 0.0, 1.0); // 1280,720
cv::Mat dist_coeffs = (cv::Mat_ <double>(4,1) << 0.01660484, -0.04549926, 0.00199781, -0.00092083); // Assuming no lens distortion
cout << "Camera Matrix " << endl << camera_matrix << endl ;
// Output rotation and translation
cv::Mat rotation_vector; // Rotation in axis-angle form
cv::Mat translation_vector;
// Solve for pose
cv::solvePnP(model_points, image_points, camera_matrix, dist_coeffs, rotation_vector, translation_vector);
// Project a 3D point (0, 0, 1000.0) onto the image plane.
// We use this to draw a line sticking out of the nose
vector<Point3d> nose_end_point3D;
vector<Point2d> nose_end_point2D;
nose_end_point3D.push_back(Point3d(0,0,5.0));
projectPoints(nose_end_point3D, rotation_vector, translation_vector, camera_matrix, dist_coeffs, nose_end_point2D);
for(int i=0; i < image_points.size(); i++)
{
circle(im, image_points[i], 3, Scalar(0,0,255), -1);
}
cv::line(im,image_points[4], nose_end_point2D[0], cv::Scalar(255,0,0), 2);
cout << "Rotation Vector " << endl << rotation_vector << endl;
cout << "Translation Vector" << endl << translation_vector << endl;
cout << nose_end_point2D << endl;
// Display image.
cv::imshow("Output", im);
cv::waitKey(0);
}


카메라의 외부파라미터인 rotation vector, translation vector가 나온 것을 확인할 수 있다.
우리가 원하는 외부파라미터인 rotation은 3x3 형태여야 한다.
rotation matrix를 구하기 위해 Rodrigues 표현법을 사용한다.


'Opencv 공부' 카테고리의 다른 글
| realsense camera calibration 캘리브레이션 (0) | 2023.03.28 |
|---|---|
| Realsense d435, d435i, l515 동시에 사용하기 (0) | 2023.03.22 |
| c++ opencv make (0) | 2023.03.11 |
| ZED 카메라 파라미터 (0) | 2023.03.11 |
| Solvepnp(camera extrinsic parameter, 카메라 외부파라미터) (0) | 2023.03.11 |


